位运算(C/C++)
[TOC]
概念
运算符
位取反运算符(~)
位与运算符(&)
位或运算符(|)
位异或运算符(^)
将两个数的比特位进行合并,返回一个新数。这两个数相同比特位不同时就返回 1。
- 位左移运算符(<<)位右移运算符(>>)
把所有位数的数字向左或者向右移动一定位数。
将一个数左移一位,相当于把这个数翻倍;将一个数右移一位,相当于把这个数减半。
已经存在的比特位按指定的位数进行左移或者右移,移动后超出存储边界的位都会被丢弃,用 0 来填充移动后产生的空白位。
原码:原码就是符号位加上真值的绝对值,即用第一位表示符号(0 为正,1 为负),其余位表示值。
反码:正数的反码是其本身;负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
补码:正数的补码就是其本身;负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1(也即在反码的基础上+1)。计算机用补码表示负数。
正数三码相同,负数的原码取绝对值,反码除符号位以外各位取反,补码为反码+1。
有符号整数
- 有符号整数使用第一位来表示该整数是正数还是负数,0 表示正数,1 表示负数。
- 其余位数存储实际的值,有符号的正整数和无符号数的存储方式所一样的,都是从 0 开始算起。
- 负数的存储方式为2 的 N(数值位的位数) 次方减去它的绝对值。
位运算的性质:幂等律、交换律、结合律、分配律、德摩根律(对偶律)、取反运算性质、与运算性质、或运算性质、异或运算性质。
逻辑移位:移位不考虑符号位。左移高位丢弃,低位补零,不溢出情况下等价于乘以2;右移低位丢弃,高位补0。
算术移位:移位考虑符号位。左移高位丢弃,低位补零;右移低位丢弃,高位补符号位,等价于除以2,可能发送精度丢失。
格雷码:任意两个相邻的代码只有一位二进制数不同。
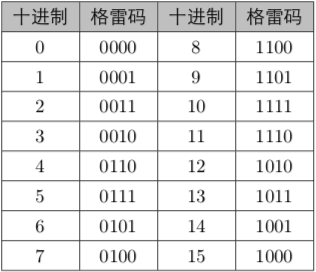
技巧
a&(a-1)的结果为将a的二进制表示的最后一个1变成0;a&(-a) (与a&(~(a-1))等价)的结果为只保留a的二进制表示的最后一个1,其余的1都变成0。
用与运算求无符号整数二进制中1的个数
用与运算判断最后一位是否为1,然后向右移位,继续判断。
进阶:为了简化这个问题,我们考虑只有高位有 1 的情况。例如:11 000 000 ,如何跳过前面低位的 6 个 0 ,而直接判断第七位的 1 ?我们可以设计 11 000 000 和 10 111 111(也就是 11 000 000 - 1)做“与”操作,消去最低位的 1 。如果得到的结果为 0 ,说明我们已经找到/消去里面最后一个 1 。如果不为 0 ,那么说明我们消去了最低位的 1 ,但是二进制中还有其他的 1 , 我们的计数器需要加 1 ,然后继续上面的操作。
1
count += num & 1; num >= 1;
用与运算判断整数是否为2的整数次幂
一个整数如果是 2 的整数次方,那么它的二进制表示中有且只有一位是 1 ,而其它所有位都是 0 。 根据前面的分析,把这个整数减去 1 后再和它自己做与运算,这个整数中唯一的 1 就变成 0 了,也就是得到的结尾为 0 。
1
return (num & (num - 1)) == 0;
用异或运算不借助临时变量,交换两个变量的值
1
a=a^b; b=a^b; a=a^b; //用两次异或交换变量值
用异或运算判断成对数字
两个相等的数异或所得的结果为0,0与任何数字异或得那一数字本身。
C/C++特性
- 可以移位的数据类型:char,short,int,long,unsigned char,unsigned short,unsigned int,unsigned long
- 不可以移位的数据类型:double,float,bool,long double
- 有符号数字左移、右移其符号位受到的影响依照编译器实现而定,即为不确定的。